
Pythagoras of Samos was an important mathematician and philosopher of Antiquity.
The proposition that can be proven logically from an axiom or other theorems that have already been respectively proven is known as a theorem . In this context it is essential to respect some rules of inference to arrive at said demonstration.
Pythagoras of Samos (582 BC–507 BC), asimismo, fue un filósofo y matemático de origen griego. A diferencia de lo que puede llegar a suponerse, Pythagoras no fue quien creó el teorema que lleva su nombre. Dicho teorema fue desarrollado y aplicado mucho tiempo antes en Babylon y la India; sin embargo, la escuela pitagórica (y no el propio Pythagoras) fue pionera en hallar una demostración formal para este teorema.
Pythagoras can also be said to be considered the first pure mathematician in history and he helped solidly in the development of scientific areas such as the aforementioned mathematics but also geometry, arithmetic , astronomy and music. And all thanks to both his aforementioned theorem and other important discoveries such as the functional significance of numbers or the incommensurability of the sides and diagonal of what the square is.
What is the Pythagorean theorem
Specifically, it can be stated that the so-called Pythagorean theorem states that the square of the hypotenuse, in right-angled triangles, is equal to the sum of the squares of the legs . To understand this sentence, we must keep in mind that a triangle that is identified as a right angle is one that has a right angle (that is, it measures 90º), that the hypotenuse consists of the longest side of said figure (and opposite to the right angle ) and that the legs are characterized by being the two smaller sides of the right triangle.
The importance of this theorem that concerns us now is that it allows us to discover a measurement based on two specific data. That is to say, it was an important step in the mathematical field because it made it possible for us to find out what the length of the third side is by knowing the lengths of two sides of a right triangle.
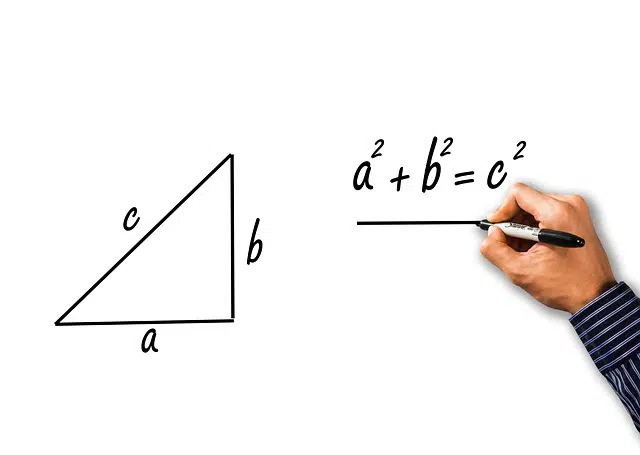
According to the Pythagorean theorem, in a right triangle, the square of the hypotenuse is equivalent to the sum of the squares of the legs.
The demonstrations
In 1927 , mathematician ES Loomis compiled more than 350 proofs of the Pythagorean theorem. Loomis classified these demonstrations into four groups: geometric demonstrations , which are carried out based on the comparison of areas ; algebraic demonstrations , developed based on the link between the sides and segments of the triangle; dynamic demonstrations , which appeal to the properties of force; and quaternionic proofs , which arise with the use of vectors.
In the case of geometric demonstrations, it should be noted that many authors or scientists have carried them out throughout history. Among them we should highlight, for example, the great philosopher Plato, who developed them in his famous dialogues, or the mathematician Euclid.
Algebraics have also led to various people deciding, in one way or another, to propose, develop and demonstrate them in a real and palpable way. Thus, in this case, it would be necessary to cite such illustrious figures as Leonardo da Vinci who has carried out the construction and demonstration of this form of the aforementioned Pythagorean Theorem.
