
The plus sign allows addition to be identified as a mathematical operation.
A sum (from Latin summa ) is the aggregate of things. The term refers to the action and effect of adding or adding . Although the concept is not always related to mathematics, through them it can be understood directly and clearly; In this science, addition is understood as an operation that allows adding one quantity to another or other homogeneous quantities.
As a mathematical operation, addition or adhesion consists of adding two or more numbers to obtain a total amount. The process also allows two groups of things to be brought together to obtain a single set.
Analyzing the operation
For example: if I have three apples and I take another two, I will have five apples ( 3+2=5 ). What was mentioned regarding homogeneous quantities refers to the fact that, if I add four pears to five apples, I will obtain nine as a result, but not nine apples or nine pears. The logical operation is the same ( 5+4=9 ), but the quantities are not homogeneous, unless the apples and pears are grouped in the set of fruits.
It is important to note that addition and subtraction are the most basic mathematical operations and the first ones learned during childhood; The simplest way to count consists of the repetitive action of adding one ( 1+1+1+1=4 ). Which in turn have their complex pair, in the case of addition their pair is multiplication and in the case of subtraction , division .
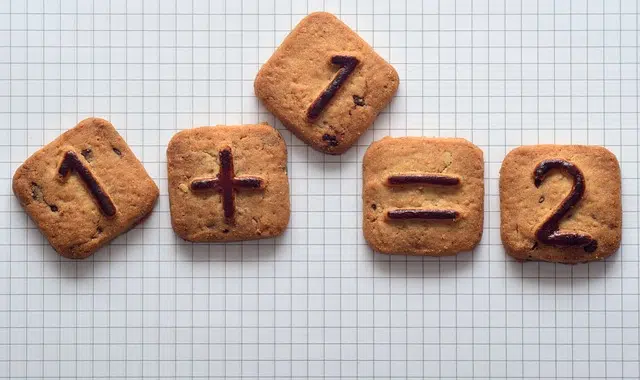
Addition allows adding quantities.
The laws of addition
The sum has various properties , which are classified within the laws that support it, which are 5 and are known by the following names: Commutative Law, Law of Uniformity, Associative Law, Dissociative Law and Law of Monogamy .
It is commutative (the order of the factors does not alter the result: 4+3=7, 3+4=7), dissociative (it is not altered if the various addends are decomposed and added in different ways. This law is considered to be reciprocal of the associative), associative (the product of several numbers does not vary if some of its factors are replaced by their product) and distributive (the sum of two numbers multiplied by a third is equal to the sum of each of these numbers multiplied by the third number). It also has a neutral element (4+0= 4, 0+8=8) and an opposite element (for any number there is another opposite whose sum results in zero).
In turn, addition allows you to add elements from different sets ; in this case, a series of steps must be taken into account in order to correctly carry out the operation.
The principle of addition
In the principle of addition, each of the elements must be carefully analyzed . The cardinal of the set is the number of elements it has and is represented by the letter A. To add the elements between two or more sets, those that are common to both must first be isolated. In this way, once the number of shared elements is known, what each set has separately must be added and these common elements subtracted. In the case of having more than two sets, the cardinal must be subtracted and finally add the intersection between all of them.
It is important to note that the concept is also present in various colloquial phrases that are not related to mathematics. For example, telling someone to do something “with great care” or “with extreme caution” means that you are asking them to do it delicately, knowing how to avoid any dangers that may arise. You can also say "In short..." as a synonym for the phrases: "At the end of the day" or "In short."
