
The breast of a woman is called the breast.
Sine , a concept with etymological origin in the Latin word sinus , has various uses. The first meaning recognized by the dictionary of the Royal Spanish Academy ( RAE ) refers to the hole , the gap or the opening of something. By extension, the idea of a sine is associated with the interior of a thing .
For example: "The native inhabitants believed that terrible monsters lived within the volcano" , "Oil gushed from the earth and nothing was the same in the region" , "We cannot allow such harmful attitudes within of our community .
Breast as female breast
The term breast also refers to a woman 's chest . In this way, the breasts can be associated with the breasts or mammary glands : "The model caused a stir by parading with her breasts exposed" , "It is important that, when showering, women feel their breasts for eventual early detection of breast cancer» , «The ball hit me in the left breast» .
From this meaning, breast is used to name the mother 's lap or everything that provides shelter, help or protection : "Doña Elvira kept her grandson in her bosom for hours, until the little one calmed down," " I am grateful to this country that welcomed me into its bosom when I arrived escaping from the war" , "When faced with a problem, a child always goes to the bosom of his mother" .
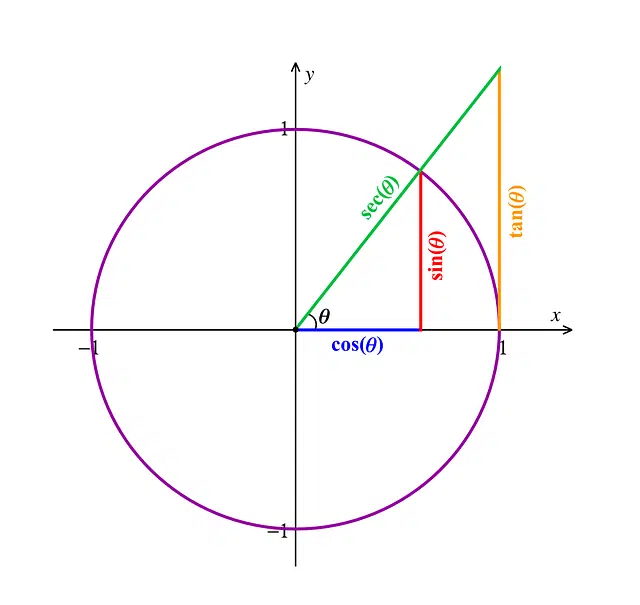
Among the trigonometric functions of right angles, the sine appears.
A trigonometric function
In the context of mathematics , sine is a trigonometric function of a right triangle, which is calculated by dividing the opposite leg by the hypotenuse. In this way, the sine of a triangle whose opposite leg measures 20 centimeters and its hypotenuse, 60 centimeters, is equal to 0.33 .
Trigonometry defines the law of sines as a proportionality relationship (that is, a constant ratio or relationship between magnitudes that can be measured) between the length of each side of a triangle and the sine of each respective opposite angle. This is also known as the sine theorem and is usually presented with the following definition: if in the triangle ABC (the names of its angles) we understand that a, b and c are the lengths of its opposite sides, we can say that a / sin A = b / sin B = c / sin C .
Angles A, B, and C can also appear as α, β, and γ (alpha, beta, and gamma), the first three letters of the Greek alphabet. It is worth mentioning that not many know its proof , even though it is very simple and is one of the most used trigonometric laws. Let us see, therefore, its proof.
Demonstration of the law
First of all we must draw the triangle ABC and denote its circumcenter O, that is, the center of its circumscribed circle , which in this case is defined as the one that passes through all the vertices of the triangle, and also draw said circle.
The next step is to draw a line that contains the segment BO and that continues until it crosses the side AC and cuts the circumference, to give rise to the diameter BP. At this point we should observe a right triangle, PCB. Angles P and A are congruent, since they are both inscribed and open BC. An inscribed angle is convex and its vertex is in a circle, in addition to being made up of semi-right chords or secants of it. All this gives rise to the following equality, according to the sine function: sin A = sin P = BC / BP = a / 2R , with R being the radius.
Finally, by solving for 2R we can obtain a/sin A = 2R and if we repeat this with two other diameters, one from A and the other from C, we can confirm that all the resulting fractions are equal to 2R.
