
The golden ratio is also known as divine proportion, golden number or golden ratio.
The golden ratio is an irrational number that ancient thinkers discovered when they noticed the link between two segments belonging to the same line . This proportion can be found in nature (flowers, leaves, etc.) and in geometric figures and is given an aesthetic condition: that which forms respect the golden proportion is considered beautiful.
This proportion, which is also often mentioned as the golden ratio , golden ratio or divine proportion , even used to be noted for its supposed mystical properties. Its equation is expressed as 1 plus the square root of 5, all over 2, and the result is approximately equal to 1.61803398874989…
A relationship between two segments
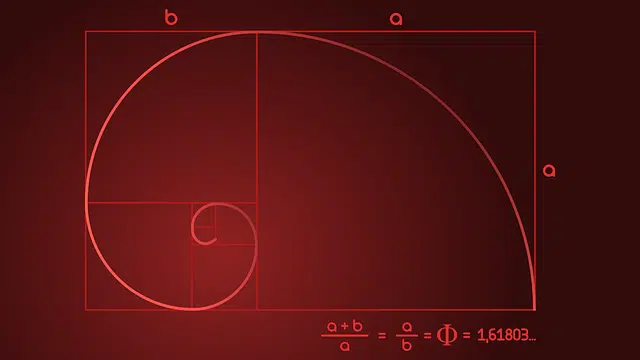
It can be said that the golden ratio arises from the relationship between a segment a and a segment b . Segment a is longer than segment b , while the total length of the line is, to segment a , as segment a is to segment b .
If we put the golden ratio into an algebraic expression, we obtain the following equation : (a + b) / a = a / b . The golden ratio, which is referred to with the Greek letter phi , is the result of the division between a and b .
Another way to understand the notion of the golden ratio consists of finding the following equivalence, also reflected in the previous algebraic expression: if we take a segment and cut it in two, the quotient of the division of the length of the line ( a+b ) and the length of the longest segment ( a ) must be identical to the quotient of the division of the length of the longest segment ( a ) and the length of the shortest segment ( b ).
The Fibonacci sequence is an infinite sequence of numbers.
Golden ratio and Fibonacci sequence
A concept closely linked to the golden ratio is the Fibonacci sequence , discovered by the Italian mathematician Leonardo de Pisa, also responsible for the dissemination of the Arabic numeral system on the European continent. This sequence presents an infinite sequence of numbers in which the addition of any pair results in the next number (0, 1, 1, 2, 3, 5, 8, 13, etc.). Curiously, if we divide any number in the Fibonacci sequence by the one that precedes it (especially starting with 5) it gives us a result that is close to the golden ratio.
Although its definition is abstract and somewhat difficult to understand, the application of the golden ratio is important in photography , painting , sculpture and other arts that usually link the ideal of beauty to symmetries and proportions.
The Golden Spiral
The graphic representation of the golden ratio, which is obtained by drawing a series of rectangles and joining some of their vertices with a spiral line , results in the well-known Golden Spiral , which is very frequently found in nature (two examples are the seashells and sunflower seeds). In photography, the use of this figure to place different objects can offer impressive results, with a harmony and fluidity that reflect the spirit of the scene.
Despite the benefits that the golden ratio can bring to photography, experts recommend using this concept as a guide, rather than turning it into a rigid structure that prevents the spontaneous and creative composition of images. Furthermore, it is important to highlight that not all cameras have the appropriate characteristics for their application (for example, due to having square sensors, since the complete spiral covers a rectangle, that is, it is wider than it is tall), and that does not mean that they are not capable of making good catches.
Likewise, the application of the Golden Spiral in painting and sculpture can elevate results, but by no means should it become the only path to the creation of artistic works .
