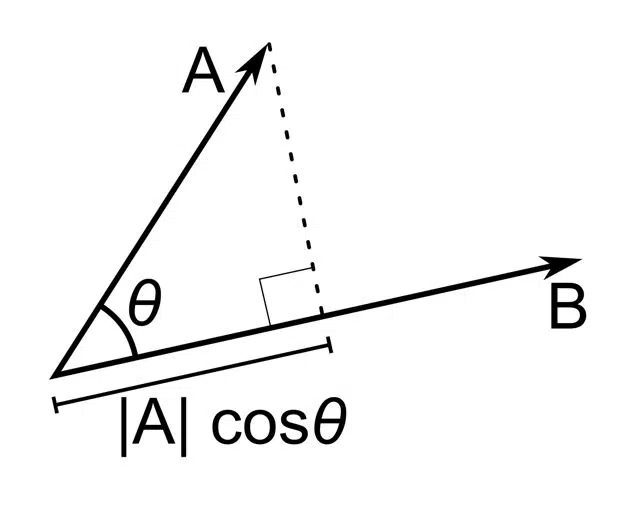
The scalar product in a Euclidean space is equivalent to that of its modules times the cosine of the angle
In the field of mathematics , the result of a multiplication is called a product . The idea of scalar , meanwhile, can be used to name the number that makes it possible to describe a phenomenon with magnitude , although leaving aside the direction of the vector.
It is important to consider before moving forward that a vector is a magnitude that requires consideration, in addition to its quantity, of its meaning, direction and point of application.
From vectors to a number
The algebra operation that starts from two numerical sequences with the same length (which usually have the form of vectors) and arrives at a single number is known as a scalar product , in this framework.
Also called the dot product , inner product , or inner product , the scalar product is obtained by adding the products of the inputs of a pair of numerical sequences. The result is not a vector, but a scalar.
It can be stated that the scalar product of a vector a→ and a vector b→ ( a→ ⋅ b→ ) results in a number (the scalar ) such that a→ ⋅ b→ = (a→) ⋅ (b→) ⋅ cos(α) , where α is the angle made up of the two vectors ( a→ and b→ ).
This allows us to maintain that, for geometry , the scalar product is the multiplication of the Euclidean magnitudes of two vectors and the cosine of the angle that they both form .
Conditions and special cases
If the vectors are parallel and share the same direction, the dot product is equivalent to the multiplication of the modules . On the other hand, if the meaning is different, it is obtained by multiplying its modules but adding the negative sign . For them to be parallel, the angle formed between them must be 0 (either sexagesimal degrees or radians) or pi radians (or 180 sexagesimal degrees). This equivalence is explained because the cosine of two parallel vectors is equal to 1, so that multiplying it by the modules does not affect their scalar product.
In the case of perpendicular vectors , the angle formed is 90º and the scalar product is equal to 0 . This is related to the fact that the scalar product can also be equal to the multiplication of the module of one of the two by the projection of the other onto it; In the case of two perpendicular vectors, the projection of one onto the other will always be 0, so no matter what the other value is, the product will also be 0.
To understand this special case a little better, let's think that the projection is similar to "the shadow" of one vector on another if the light source is perfectly perpendicular to the second; since this shadow would be imperceptible (of zero extension) if the first one were parallel to the beam of light. In more technical terms, mutually perpendicular vectors are also known as orthogonal . Going in the opposite direction, if we know that the dot product of two vectors is zero, we can assume that they are orthogonal vectors.
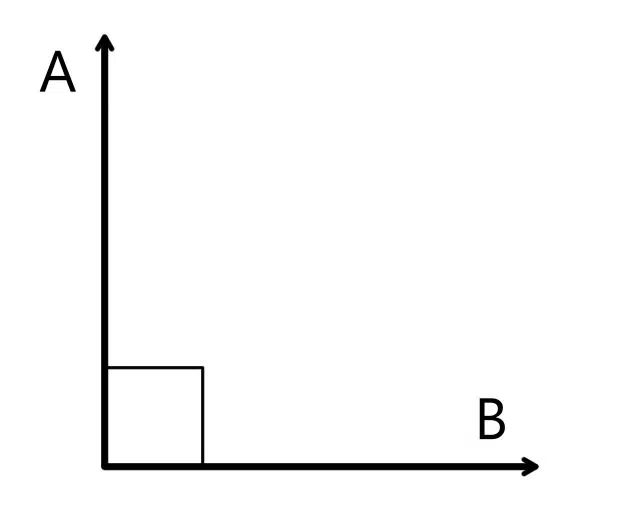
If the vectors are perpendicular, the scalar product is 0
Properties
The scalar product is still the result of a multiplication , even if it is more complex than that of two or more natural numbers , for example. Therefore, both operations share the following properties: commutative, distributive and associative . The first of the three is the best known and easiest to understand: it states that the order of the factors does not alter the product. In other words, we will obtain the same result whenever we multiply the same vectors, regardless of their order.
The second requires the multiplication of one vector by the sum of two or more. In this case, it is possible to extract the addends one by one, multiplying them by the first vector and creating a sum of these products that will be equivalent to the first equation : A. (B + C) = A. B+A. C Finally, the associative property tells us that if we have the multiplication of a scalar by a product of two vectors, it is possible to convert the equation into the product of said scalar by any of the vectors and then multiply it by the remaining one: e(B . C) = eB. C = B. eC
