
A Cartesian plane is formed with a pair of mutually perpendicular axes (the X axis and the Y axis) that are interrupted at the same point of origin.
A Cartesian plane is an ideal element that has Cartesian coordinates . These are lines parallel to the axes that are taken as reference. They are drawn on the aforementioned plane and make it possible to establish the position of a point . The name Cartesian plane, of course, is a tribute to René Descartes , who sustained his philosophical development from a starting point that was obvious and that allowed knowledge to be built.
Before moving forward, we are going to proceed to establish the etymological origin of the two words that give shape to the concept. Thus, plane emanates from the Latin planus , which can be defined as "flat." The notion has various uses and meanings: it can be a surface that lacks reliefs, elevations or undulations ; of an element that has only two dimensions and that houses infinite points and lines ; or a scheme developed to scale that represents a piece of land, a building, a device, etc.
Cartesian , for its part, is an adjective that derives from Cartesius , the Latin name of the aforementioned French philosopher Descartes (who lived between the end of the 16th century and the first half of the 17th century ). The term, therefore, refers to what is linked to Cartesianism (the postulates or principles proposed by this thinker).
Cartesian plane concept
The Cartesian plane exhibits a pair of axes that are perpendicular to each other and are interrupted at the same point of origin . The origin of coordinates, in this sense, is the reference point of a system : at said point, the value of all the coordinates has zero ( 0, 0 ). The Cartesian coordinates x and y , on the other hand, are called abscissa and ordinate , respectively, in the plane.
In a plane coordinate system, which is formed by two perpendicular lines or straight lines that intersect at the origin, each point can be named by two numbers .
In the same way, we cannot ignore another series of elements that are fundamental in any Cartesian plane. In this way we find the origin of coordinates , which is represented by the O and which can be defined as the point at which the aforementioned axes intersect.
Likewise, reference must also be made to what is called the abscissa of point P and the ordinate of point P. And all this without forgetting either that in any Cartesian plane various functions can be carried out such as linear ones, those of direct proportionality and those of indirect proportionality .
The Cartesian plane is important in linear algebra, analytical geometry, trigonometry, and other fields of mathematics.
The quadrants
A Cartesian plane is divided into four quadrants . In the upper right part is the first quadrant , where the positive numbers of the two axes are found.
In the upper left sector of the Cartesian plane, there is the second quadrant , with the negative numbers of the X axis and the positive numbers of the Y axis. The third quadrant is located in the lower left area, covering the negative numbers of both the X axis and the Y axis.
Finally, in the lower right part, the fourth quadrant appears, collecting the positive numbers on the X axis and the negative numbers on the Y axis.
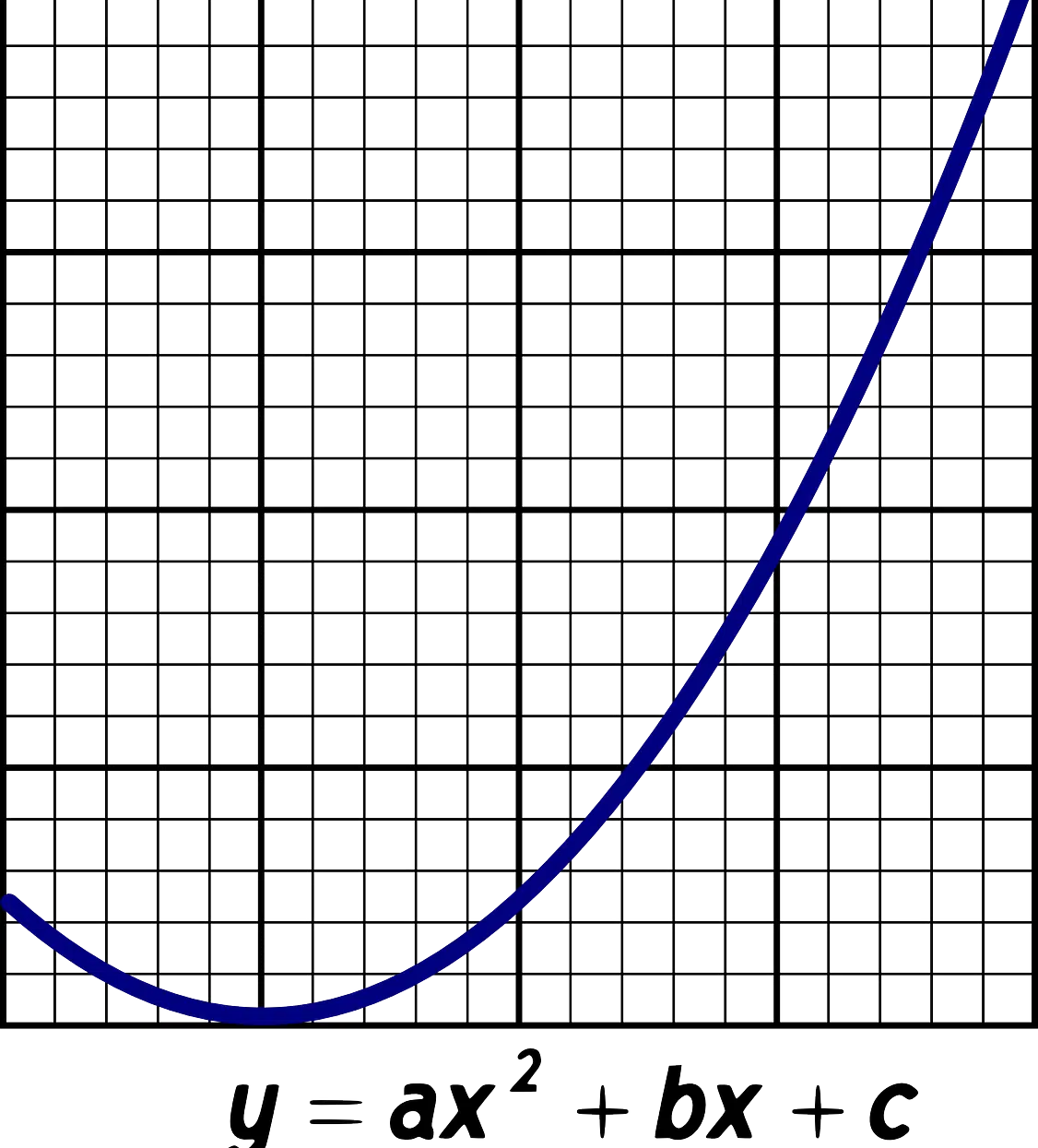
Various functions can be expressed in a Cartesian plane.
Functions in a Cartesian plane
Linear functions are identified by the fact that all points in them are aligned. Meanwhile, direct proportionality functions are characterized by the presence of what is known as the proportionality constant, which is identified by the letter k , and by the fact that in them if in pairs of values the ordinate is divided by the abscissa always obtains the same number.
This is an operation that differs from the one that occurs in indirect proportionality functions because in them what occurs is the multiplication of the ordinate by the abscissa in the pairs of values. The result, then, will always be the same number.
Other classifications refer to trigonometric functions , exponential functions , logarithmic functions , rational functions and irrational functions , to name a few.
Probability distribution
In a Cartesian plane, the probability distribution can be expressed, a function that implies the assignment of the probability of occurrence to each event that is defined on a random variable. Depending on their characteristics, there are different types of distributions.
Before moving forward, we must keep in mind that a random variable is associated with results that arise by chance in any event. If it can only take on specific values (usually integers), it is called a discrete random variable , while a continuous random variable can take on any value in a certain interval.
According to this class of variables, the probability distribution can be divided into different groups. Discrete variables correspond to a discrete distribution , which can be a hypergeometric distribution , a poisson distribution or a binomial distribution .
In the case of continuous random variables, they generate a continuous distribution . In this set there are the exponential distribution , the Cauchy distribution and the Gaussian distribution or normal distribution .
