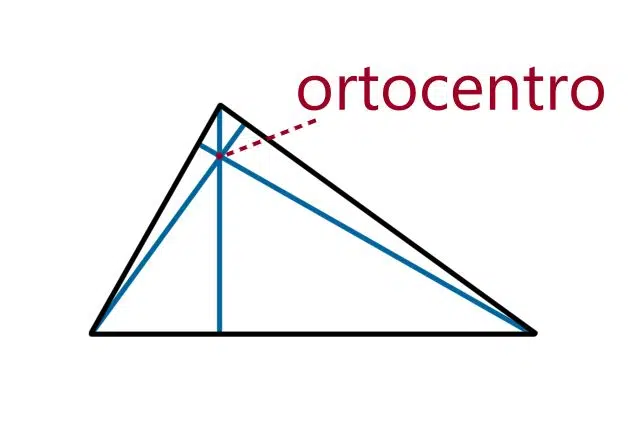
The heights of the triangle converge at the orthocenter.
The notion of orthocenter is used in the field of geometry . This is the name given to the point where the heights of a triangle intersect .
Orthocenter location
The point at which the three heights intersect is the orthocenter. Since it is not an arbitrary point within the figure, but one that can be found through exact calculations, it can be used as a reference as well as the vertices to locate the triangle in space, for example. The location of the orthocenter depends on the characteristics of the triangle.
In an obtuse triangle (which has one obtuse angle and two acute angles), the orthocenter is outside the figure. If the triangle is right angled (it has a right angle ), the orthocenter is coincident with the vertex of the 90° angle . In the case of acute triangles (all angles are acute), the orthocenter is located inside the figure.
In summary, it can be said that, in triangles, the height is a line that passes through a vertex and is perpendicular to the opposite side. Each of the triangles has three heights: the point where the heights meet is called the orthocenter, which can be located inside or outside the triangle itself.
In equilateral triangles (whose sides measure the same), the orthocenter, the circumcenter, the centroid and the incenter coincide at an interior point that is at an identical distance from the three vertices. In non-equilateral triangles , however, the orthocenter, the circumcenter and the barycenter are positioned aligned and included in the so-called Euler line . A property indicates that the distance from the orthocenter to the barycenter doubles the distance between the barycenter and the circumcenter.
Triangle heights
It is important to note that each triangle has three heights . These heights are the lines that allow a vertex to be joined to its opposite side , being perpendicular to said sides.
The triangle is a figure that is as used as it is particular, since at first glance we can consider it "simple" because it is easy to draw. However, when we analyze it from a mathematical point of view, the level of complexity increases considerably. For example, while to calculate the surface area of a rectangle it is enough to multiply two of its sides (that are adjacent), in the case of a triangle we must multiply its base by its height and then divide the result by 2.
Now, we just mentioned the term "height" as a singular property of the triangle, despite the fact that above we talked about the three that this geometric figure has. The solution to this confusion is very simple: we must arbitrarily choose one of the three to assign its value to the variable height of the equation, and the perpendicular side of it becomes the base .
Note that this height must convert the triangle into two right-angled triangles, so it is only possible to find it in the other types: for right-angled triangles, their base and height coincide with their minor and greatest legs, respectively.
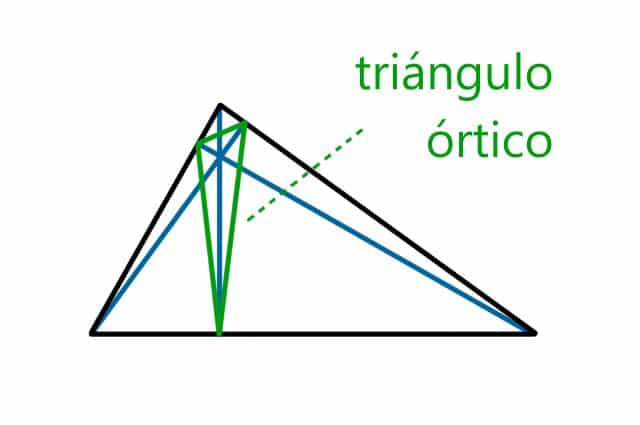
"Orthic" or "pedal" triangle as shown above
Orthic triangle
One of the peculiarities of the orthocenter is that it allows us to determine a new triangle within the main one. This is the orthic triangle , which is formed by joining the three points from which the previously defined heights start. Another name for this figure is pedal triangle , and it cannot be generated in a right triangle.
These points are also called feet , and are the projections of each of the three vertices on its opposite side. Above we talked about incenter (the point at which the bisectors of the internal angles intersect); since the incenter of an orthic triangle coincides with the orthocenter of the one that contains it.
