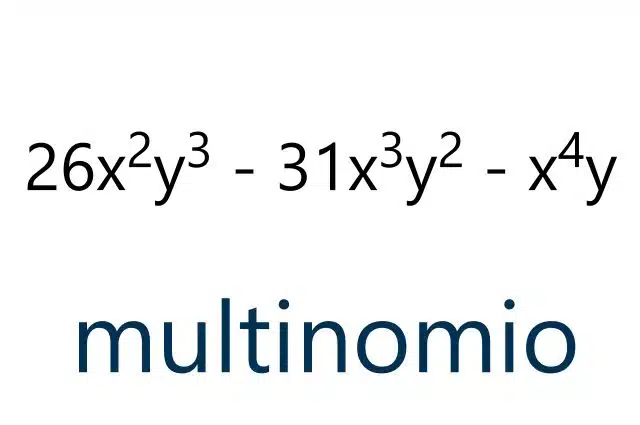
Example of a multinomial
The notion of multinomial is used in the field of algebra to refer to an expression that contains two or more terms . To understand its meaning, therefore, you must first know what algebra is and what its expressions are.
Algebra and arithmetic
Algebra is the branch of mathematics dedicated to the study of abstract structures . In these structures, signs , letters and numbers are used to generalize arithmetic operations .
While arithmetic revolves around numbers and fundamental operations, algebra adds letters to develop the representation of unknowns (which are unknown quantities) and parameters (which can be coefficients or variables). In this framework, the expressions that are formed are called algebraic formulas .
The multinomial
Returning to the idea of multinomial, it is a quantity that is expressed by two or more terms in the same formula. An algebraic term , meanwhile, is a product of factors that is represented by letters and numbers.
When all the terms are integers and rational and are joined by the minus ( – ) or plus ( + ) signs, the multinomial is called a polynomial . That is why it can be said that a polynomial is a specific type of multinomial.
We can also differentiate these two concepts by taking into account that the terms of the polynomial must result in natural numbers or zero, while in multinomials, the variables can be found in radicals . This does not necessarily indicate that the complexity of the multinomial is always greater than that of the polynomial, but this is usually due to its greater breadth in the types of values it admits.
It is important to differentiate between multinomials, monomials and binomials . While multinomials have several terms, monomials only have a single term. A binomial, on the other hand, is an expression consisting of two algebraic terms related by minus or plus signs.
Multinomial theorem
In the field of mathematics there is a concept related to multinomials that is known as the multinomial theorem . This is the expansion of the power of a sum, so that it can be expressed as the powers of its terms. Its basis is found in the binomial theorem , which in this case is generalized for use in polynomials or multinomials.

The multinomial theorem is a generalization of the binomial theorem.
With respect to this last theorem, it is a formula that allows us to develop the nth power of any binomial, as long as the quantity (which is represented by the variable n ) belongs to the set of positive integers, that is, it does not include fractions or decimal numbers. What it proposes is the expansion of the power (x + y) n in the following sum of terms ax b and c , the exponents b and c being natural numbers whose sum is equal to n . Generally, if an exponent is zero, the power it affects is omitted, since its result is 1 and it does not alter the result of the binomial, multinomial or polynomial.
Returning to the multinomial theorem specifically, if we have a positive integer and one that is not negative, to which we can assign the variables m and n , respectively, thanks to this formula we can observe the expansion of the sum of m terms when we raise everything to the power n. Just as in the case of the binomial, if the exponent is zero, the power is usually left out, also if the base is equal to zero. Finally, since this theorem is based on the binomial one, if the number of terms is equal to two, this one applies.
