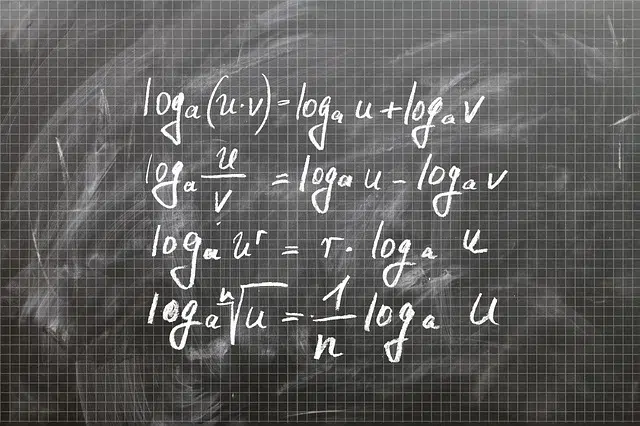
A logarithm is an exponent to which a positive quantity must be raised to obtain a certain number as a result.
The etymology of logarithm takes us to two Greek words: lógos (translated as “reason” ) and arithmós (translatable as “number” ). The concept is used in the field of mathematics.
A logarithm is the exponent to which a positive quantity needs to be raised to obtain a certain number as a result. It should be remembered that an exponent, meanwhile, is the number that denotes the power to which another figure must be raised.
In this way, the logarithm of a number is the exponent to which the base must be raised to reach said number . Many times an arithmetic calculation can be done more simply by using logarithms.
logarithm example
Let's see an example . The base 5 logarithm of 625 is 4 , since 625 is equal to 5 to the power 4 : 5 x 5 x 5 x 5 = 625 .
Given a number (the argument ), the logarithm function is responsible for assigning an exponent (the power ) to which another fixed number (the base ) must be raised to obtain the argument. Returning to our example, the argument is 625 , the power is 4 and the base is 5 .
Base to power = Argument
5 to the power of 4 = 625
5 x 5 x 5 x 5 = 625

Logarithms are studied in mathematics.
The contributions of Napier and Euler
The Scotsman John Napier is noted as the pioneer in defining logarithms in the 17th century . Years later, the Swiss Leonhard Euler linked them with the exponential function.
With the aim of facilitating operations, engineers and scientists from different fields use logarithms on a daily basis.
Logarithm of a physical quantity and measurement scale
A logarithmic scale , on the other hand, is a measurement scale that uses the logarithm of a physical quantity to replace the quantity in question.
The concept of measurement scale is also known as measurement level and is a variable that serves to describe the nature of the data that contains the numbers that are assigned to objects and, therefore, those that a variable contains.
With respect to a physical quantity , it means one that can be measured in the context of a physical system , that is, to which it is possible to assign different values based on a measurement.
Although the name may seem unusual, we have all used the logarithmic scale in school even without knowing it. For example, it can be seen in the divisions of the Cartesian axes that are separated by equal distances such as: 1, 10, 100, 1000, instead of 1, 2, 3, etc. This can be ideal for graphing data that spans a considerable range of values, as the range becomes much easier to manipulate.
The most commonly used logarithm bases are the number e , the base of natural or natural logarithms, and 10 , the base of decimals.
The link between physical stimuli and their magnitude
Thanks to the scientific studies of people like Ernst Heinrich Weber and Gustav Theodor Fechner , from the late 18th century and early 19th century, respectively, we know that there is a quantitative relationship between the way we perceive physical stimuli and their magnitude . This theory was proposed in 1860 and, in other words, it can be expressed as that certain human senses work in a logarithmic manner .
This can help us understand some of the advantages of using logarithmic scales when representing certain values, since our brain understands the concept of logarithm in a much more natural way than we think. The ear, for example, is capable of perceiving equal differences in the pitch of sounds when stimulated by equal ratios of frequencies.
As if this were not enough, some studies carried out on groups of young children and adults from tribes far from large cities have proven that human beings make use of logarithmic scales naturally to represent numerical values .
