The hyperbola is a curve with two foci and symmetrical about two mutually perpendicular axes.
The Greek word hyperbolḗ came into Latin as hyperbŏla . The concept arrived in our language as a hyperbola , a term used in the field of geometry .
Curve
A curve with two foci that is symmetrical with respect to a pair of mutually perpendicular axes is called a hyperbola. To draw a hyperbola, a right cone is cut with a plane, generating an angle smaller than that formed by the generatrix with respect to the axis of revolution.
A hyperbola has two open branches . Both are directed in opposite directions, approaching two asymptotes indefinitely. This means that, considering two fixed points, the difference in their distances is constant.
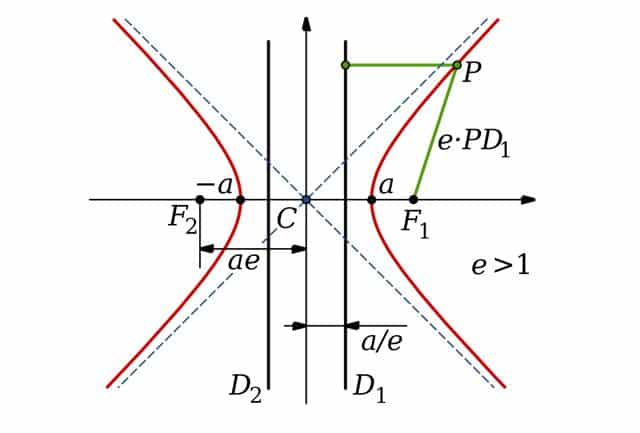
According to the smaller or larger opening of the branches of the hyperbola, its eccentricity is calculated. This eccentricity is known by dividing half the focal axis distance by half the major axis distance.
Its general equation is Ax 2 – Cy 2 + Dx + Ey + F = 0 . Note that in mathematical equations we must interpret parts like Ax or Ey as the multiplication of the two variables. If A and C are greater than 0 and their coefficients have opposite signs, then we are looking at the representation of a hyperbola with axes parallel to the coordinates.
Elements of the hyperbola
A formal definition indicates that considering two points ( F1 and F2 ) that are called foci , the hyperbola is the set of points in the plane in which the absolute value that is recorded when considering the difference in their distances to the foci (those mentioned F1 and F2 ) is constant.
In addition to the foci, it is possible to recognize other elements in the hyperbola. Among them appear the focal axis (the line that passes through both foci), the secondary axis (the bisector that joins the segment that goes from one focus to another), the center (the point of intersection of these axes) and the vertices.
Related concepts
Below we will see a brief definition of some of the complementary concepts mentioned above. Let's start with asymptote , the name given to a line to which the graph of a given function continuously approaches; In other words, the distance between the two tends to zero, although they extend indefinitely. It can also be said that its behavior is asymptotic. An example of this can be seen in rational functions.
We have also talked about a generatrix , a line that, due to its movement, is seen as a geometric figure. It can be a curved line (that generates ellipsoids, spheres, etc.) or a straight line (that rotates with respect to an axis of rotation to form cylindrical or conical surfaces, among others). One of the most important concepts in this context is focus , which belongs to the field of geometry and can be linked to a surface or a curve. It is a point that does not usually belong to these, although it does allow certain constant distances to be maintained with all its points.

In the third type of conic section we can see a hyperbola.
First uses in history
The discovery of conic sections was carried out by Menechmus , born in Greece in 380 BC. C. and specialized in mathematics and geometry. The context of such a milestone was his research on the duplication of the cube , a problem that led him to demonstrate that it could be solved by cutting a parabola with a hyperbola, something that was later confirmed by Proclus and Eratosthenes .
Although Menaechmus used hyperbola in his work, it took about a century until someone coined the term. And it was the Greek mathematician and astronomer Apollonius of Perge , who included it in his treatise titled Conics , one of the most important writings of the time.
