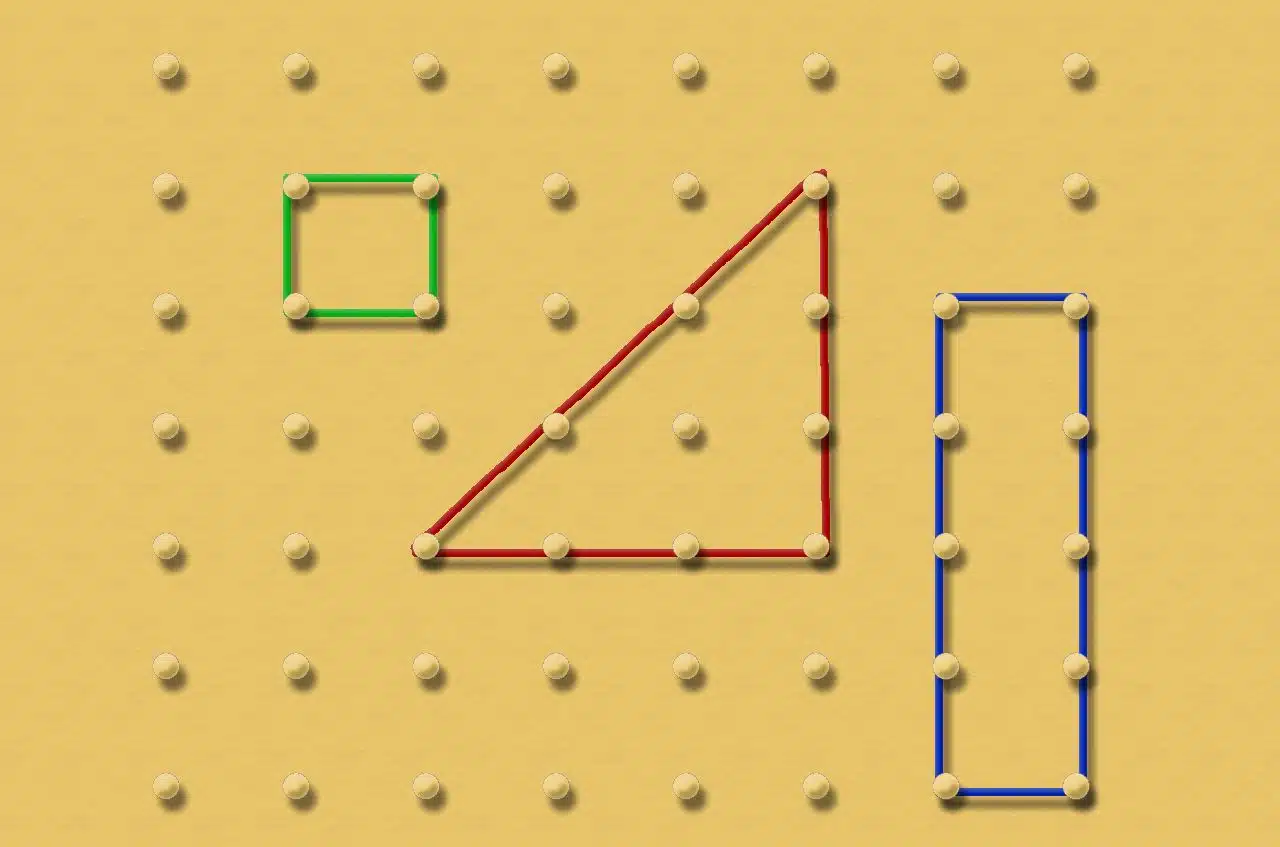
Children can learn different aspects of geometry with a geoboard.
The geoboard is a device used for teaching geometry . It is a board with pivots that allow you to create different figures.
Origins
The geoboard was created by Egyptian mathematician and educator Caleb Gattegno in the 1960s . Its intention was to offer a resource to facilitate the learning of geometry in a manipulative way: that is, allowing students to establish some type of physical contact with abstract concepts.
The first geoboard was a wooden board with a pattern made of protruding nails . Elastic bands were attached to these nails to represent the various geometric figures .
Geoboard Features
The geoboard allows children to build geometric shapes, but also learn about perimeters and areas , investigate the properties of polygons and even work on solving mathematical problems.
Currently, geoboards are usually made of plastic, although wooden boards are also still produced. There are square geoboards and rectangular geoboards depending on the shape of the board, with pivots that are arranged in different ways.
Depending on how the pivots are distributed on the board, it is possible to recognize different types of geoboards. Circular geoboards present the pivots arranged in circles. Triangular geoboards , meanwhile, have triangular plots, while orthometric geoboards are the most popular with their gridded plots.
It is important to note that you can not only get geoboards in stores. With few materials, it is easy to build geoboards at home and thus help children study mathematics .
Circular geoplan
The circular geoboard is a mathematical tool that consists of a circular disk divided into equal sections, usually 24 or 36. These serve as anchor points to place elastic bands or rubber bands that are used to create geometric shapes and explore mathematical concepts.
It is especially useful for working with symmetry, fractions, and angles . By stretching rubber bands between different anchor points, students can create shapes such as circles, ellipses, regular and irregular polygons, and explore how they transform and relate to each other.
Additionally, the circular geoboard allows children to observe how the angles change as the placement of the rubber bands varies and how sections of the circular geoboard can be divided to represent different fractions.
Triangular geoboard
The triangular geoplane is a mathematical resource used in education to explore geometric concepts and develop skills in areas such as symmetry , congruence, areas and perimeters, and the graphical representation of figures .
It consists of a triangular panel with a series of equidistant holes in the shape of equilateral triangles. Students can use the triangular geoboard to create and explore various shapes , such as triangles, quadrilaterals, pentagons, and hexagons. They can also create symmetrical figures with respect to an axis or superimpose figures to verify their congruence .
Additionally, the triangular geomap allows you to visualize and experiment with areas and perimeters. By counting the holes occupied by the elastic bands, children can determine the number of area and perimeter units of the figures constructed.
Orthometric geoplan
The orthometric geoboard is a variant of the traditional geoboard used to explore geometric concepts in three dimensions . Unlike the traditional one, which is two-dimensional, this one adds a third dimension by adding vertical columns or bars that connect to a base.
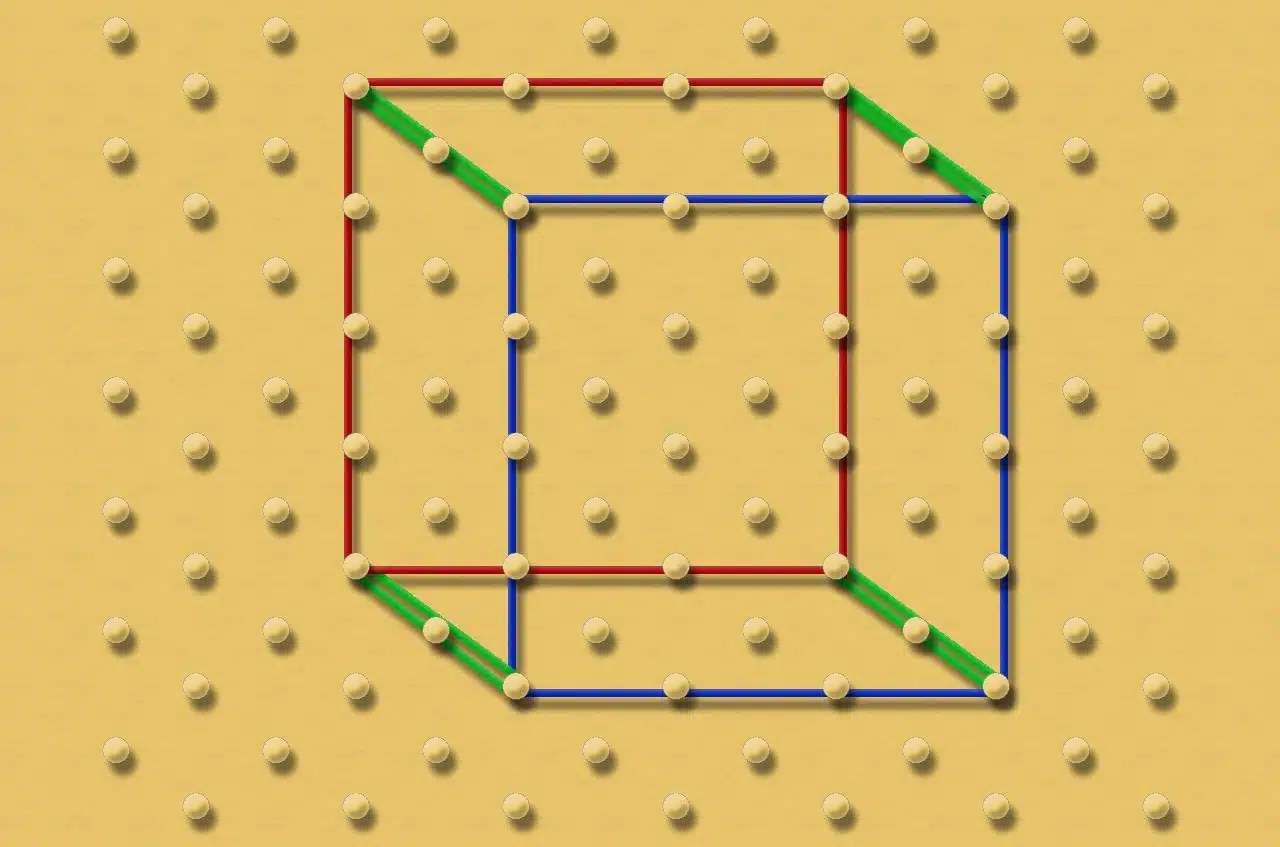
The orthometric geoplane allows the creation of three-dimensional figures.
This geoboard allows students to construct and visualize three-dimensional figures, such as cubes, prisms, pyramids, and other geometric solids. Elastic bands are placed around bars to create faces of solids and explore their shape, structure and properties.
The orthometric geoplan is a valuable tool for developing spatial skills and three-dimensional understanding . Children can manipulate the elastic bands to transform geometric solids, explore symmetries, observe changes in areas and volumes as the figures are modified, and experiment with concepts such as congruence and similarity.
