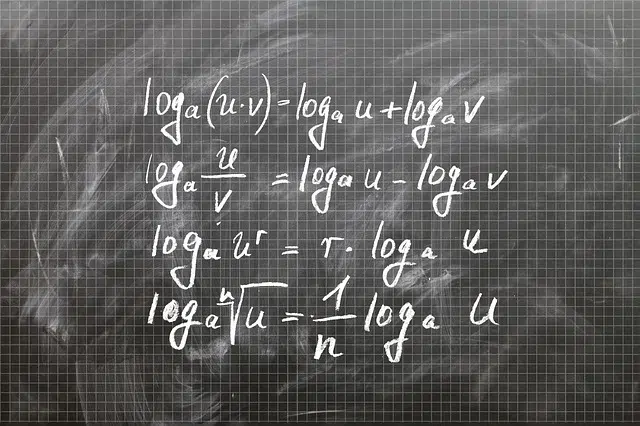
The logarithmic function can be defined as the inverse function of the exponential.
The concept of function has multiple uses. If we focus on mathematics , a function is a relationship that exists between two sets, whereby each element of the initial set is assigned a single element of the final set (or none). Logarithmic , for its part, is that linked to a logarithm : the exponent to which a certain amount needs to be raised to obtain a certain number as a result.
From these ideas , we can advance in the definition of a logarithmic function . In these functions, a is the base, which must be positive and different from 1 . The official way to read this equation is: "the function of x is equal to the base logarithm a of x." It is worth mentioning that it could also be expressed without the use of the expression f(x) , but with a variable such as y , since in this way we could reflect more clearly that the result is a different element, from another set .
It is important to note that the logarithmic function is the inverse function of the exponential function : the one that is represented with the equation f(x) = aˣ
Characteristics of a logarithmic function
Among the main characteristics of a logarithmic function, we can mention that its domain (its starting or initial set) is the positive real numbers . It is a continuous function , whose path is R (the images obtained by applying the function correspond to any of the elements of the set formed by real numbers).
Another property is that the logarithmic function of the base is equal to 1 in all cases. Logarithmic functions, on the other hand, can be increasing or decreasing, as well as convex or concave, depending on the value of the base. To know if they are increasing, just observe if a is greater than 1; On the other hand, if it is greater than 0 and less than 1, then it is decreasing.
Continuing with the properties of the logarithmic function, we can say that in the graph we always find the following two points: (1, 0) and (a, 1), understanding these pairs as values on the X and Y axes, that is, the horizontal and the vertical, respectively. The logarithmic function is also considered injective .

The logarithmic function of the base is always equal to 1.
The injective functions
In the field of mathematics, the name injective function is known as one in which each element of the codomain corresponds to only one of the domain. In other words, in a function of this type, to which the logarithmic also belongs, it cannot be the case that more than one element of the first set has the same image.
When graphing a logarithmic function we obtain a result symmetrical to that of the exponential function if we take into account the bisector of the first and third quadrants. A bisector is understood to be the ray that begins at the vertex of an angle and cuts it into two identical parts. The reason for this phenomenon is that both are inverse or reciprocal of each other.
The logarithmic function and the base or argument
Logarithmic functions, in short, are those in whose equation the variable is the base or argument of a logarithm. To solve these equations, it is generally a matter of converting the logarithmic equation into another that is equivalent but does not have a logarithm.
In some cases, the conversion sets the base of the logarithm to the power of x and sets this term equal to y . For example, if we have a function of x in which the base is 2, for each element of the codomain we must find what number is equal to it if we square it.
