
A fraction allows us to express a division: 1/8 of a pizza, for example, refers to one of the eight portions into which this food can be divided.
Originating from the Latin fractio , the concept of fraction gives its name to a process based on dividing something into parts . In the field of mathematics , the fraction is an expression that marks a division. For example: 3/4 , which is read as three quarters , indicates three parts out of four totals, and can also be expressed as 75% .
The fraction, therefore, states what quantity must be divided by another number. If I add 1/4 to 3/4, I will get 4/4, that is, 1 (an integer ). Fractions that have identical value (such as 3/6 and 5/10) are known as equivalent fractions .
Fractions are made up of numerators and denominators . In 1/2, 1 is the numerator and 2 is the denominator. These components are always integers ; Therefore, fractions can be included in the group of rational numbers .
Classification of fractions
Depending on the type of link established between the numerator and the denominator, fractions can be classified as proper (if the denominator is larger than the numerator), improper (when the numerator is larger than the denominator), reducible (when the numerator and the denominator are not prime to each other, a particularity that allows the structure to be simplified) or irreducible (those where the numerator and the denominator are prime to each other and, for that reason, it cannot be done more simple).
Mixed fractions have a particular appearance, since a whole number is written in front of the numerator and denominator, generally larger (in terms of its typography) and located in the vertical center . This value indicates how many times the denominator is completed, a fact that does not happen in the rest of the fractions. An example would be 4 1/3, which means you have 4 ones (four times three thirds) and one third.
Homogeneous fractions are those that share the denominator (5/8 and 3/8). Heterogeneous fractions , on the other hand, have different denominators (3/5 and 7/9).
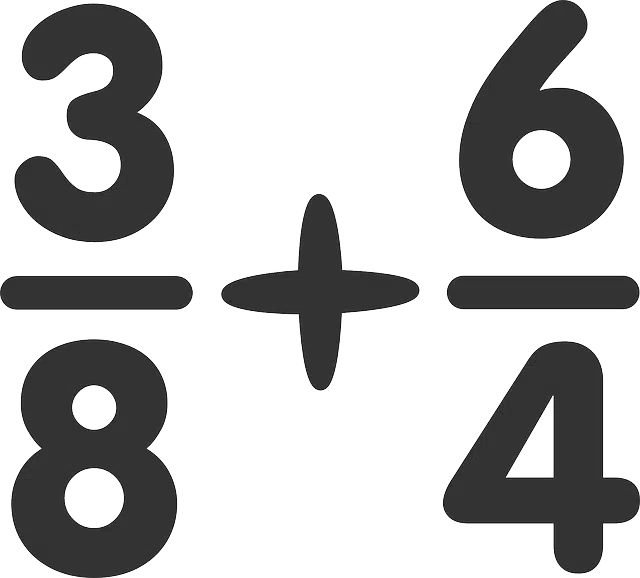
Operations with fractions require taking into account several issues.
The operations
Operations with fractions do not present great complexity. However, they are not as direct as, for example, those of integers. In principle, in the case of addition and subtraction, if the denominator of the fractions is the same, the procedure does not have any particularity that makes it difficult to understand. If we have 5/10 – 3/10, the result will be obtained by making the difference between 5 and 3, which will give us 2; the 10 will remain intact. Likewise, adding 5/10 and 3/10, the result will be 8/10.
If the denominators were different, it would be necessary to find the least common multiple between them, since otherwise it would be impossible to perform the desired operation. The procedure, accompanied by an example, is found in our definition of subtraction . A good practice is to take each fraction to its irreducible state before and after any calculation. To do this, we need to know the greatest common factor of the denominator and the numerator.
In the case of the fraction 6/24, for example, after using one of the known methods to find the greatest common divisor, such as decomposition into prime factors or Euclid's algorithm , we will find the following reduced fraction: 1/4 . The value by which both 6 and 24 can be divided without obtaining results that exceed the limits of integers is 6.
Multiplication is perhaps the simplest operation; If we have 4 x 2/15, where 4 can be interpreted as 4/1, the result will be obtained by performing 4 x 2 and 1 x 15 and will be 8/15, which cannot be reduced. Division is a little tricky at first, since it is equivalent to multiplying the first function by the opposite of the second; that is, 4/15 : 7/12 is the same as 4/15 x 12/7.
Finally, it should be noted that groups that are part of a larger organization , but that differ from each other or from the whole, are called a fraction.
