Elimination is the act and result of eliminating . This verb (eliminate), in turn, refers to suppress, delete, exclude or remove . For example: “The elimination of the subsidy will cause a 35% increase in the electricity rate” , “The Venezuelan team must win or win to avoid the elimination” , “My nutritionist suggested a diet aimed at eliminating fat” .
The idea of elimination is usually used in the field of sports . In this case, elimination takes place when, due to a defeat or position in the standings, the participant of a tournament can no longer participate and is excluded from the competition .
Tennis tournaments have a competition system based on direct elimination : at the end of a match, the winner continues to advance while the loser is eliminated. The soccer World Cups , for their part, appeal to the same system after the first phase. France 's elimination from Brazil 2014 , to name one example, occurred when it lost 1-0 to Germany in the round of 16.
In the context of health , bodily elimination is given by a series of physiological processes that enable the excretion of waste through sweating, defecation and urination.
Drug elimination , on the other hand, involves the expulsion of a drug through the action of the kidneys, liver or other organs. The elimination routes are varied and depend on each case.
In the field of mathematics, there is an algorithm called Gauss-Jordan elimination , which is used in linear algebra to find solutions to a system of linear equations, find inverses and matrices. It takes its name from its creators, the German scientists Carl Friedrich Gauss and Wilhelm Jordan , and should not be confused with Gauss's method, although they are similar.
Thanks to this elimination method, it is possible to solve a system of equations by reducing it to another equivalent, in which the equations have one less unknown than the first. In this way, we can transform the coefficient matrix into an upper triangular one, until we get a diagonal.
It is important to mention that already in The Nine Chapters on the Mathematical Art , a very important Chinese book dating from the 2nd century BC. C., the use of this method is illustrated throughout almost twenty problems, which means that Gauss and Jordan were not the first to discover it.
Regarding the computational complexity of this elimination method, that is, the number of operations that we must perform to put it into practice, it is around n to the power of three , if the matrix has a size nxn .
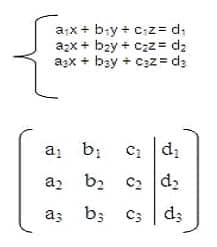The Gauss elimination and the Gauss-Jordan elimination are useful when we find a system of equations like the following:
2x + y – z = 8
-3x – y + 2z = -11
-2x + y + 2z = -3
Since we have so many unknowns, we cannot solve them simply by passing them from one term to another (known as solving ). Therefore, we must perform operations between the equations to reduce the number of unknowns until we find the three results we are looking for. To do this we must follow the foundations of this theory, which are summarized in the following three operations, called elementary :
* take a scalar that is not null and multiply it by one of the equations;
* exchange the positions of two equations ;
* take a multiple of one equation and add it to another.
We cannot always apply this elimination method to solve systems of equations, since some are incompatible. We recognize them when the result of an equation is a number other than 0, even though it should be 0.