
Erwin Schrödinger was the physicist who developed an extremely relevant equation within ordinary quantum mechanics.
Schrödinger's equation is the name given to a key foundation for quantum mechanics with a non-relativistic approach that, at first, was considered as a simple equation of motion based on a material field whose propagation had a wave format. According to scientific experts, this development can be understood as equivalent, but at a quantum level, to the value that Newton's laws (specifically, the second principle) have within classical mechanics .
This is a contribution made in 1925 by Erwin Schrödinger , a philosopher and physicist of Austrian origin who became naturalized Irish. In 1933, in the same year as Paul Dirac , Erwin was awarded the Nobel Prize in Physics .
The equation that bears his surname (also present in the name of a thought experiment popularized as Schrödinger's cat ) is used in numerous disciplines and activities, although in relativistic scenarios it is usually replaced by treatments linked to quantum field theory .
Characteristics of the Schrödinger equation
As noted when reviewing the theory, the Schrödinger equation (which has been classified as a partial differential equation in which linear operators appear) allows us to describe, in a non-relativistic framework, what it is like, from a temporal point of view, the evolution of subatomic particles (a set that groups together elementary and compound particles) that are quantum with mass.
Each physical situation must be taken into account to establish what form said equation will take according to the circumstances. The most widespread structure represents a system that evolves over time through a time-dependent Schrödinger equation . They appear in it, for example, Planck's constant , the wave function corresponding to the quantum system and the Hamiltonian operator .
There is, in the same way, a Schrödinger equation that is independent of time. It is used to predict the probability that a wave function exhibits the appearance of a standing wave . It is a variant that is characterized by describing a stationary state , as long as the Hamiltonian is not dependent on the time issue.
When focusing on the particularities of the Schrödinger equation, it is advisable not to overlook the limitations it presents. In this sense, it is enriching to know that it is a non-relativistic equation reserved for working with particles that, compared to the value resulting from the energy at rest when divided by the speed of light , reflect a small linear momentum. If this requirement is not met, then alternatives such as the Klein-Gordon equation or the Dirac equation gain prominence. There are also failures to properly incorporate the spin of each particle . For this reason, Wolfgang Pauli reformulated it through the so-called Schrödinger-Pauli equation or simply the Pauli equation , where the interaction involving the electromagnetic field and spin is contemplated.

The Schrödinger equation has a similar role or value in quantum mechanics to that of Newton's second law within classical mechanics.
Applications
The Schrödinger equation has multiple applications. It is a useful tool, for example, within semiconductor physics , as well as being an object of interest for those who are dedicated to cryptography or the field of microelectronics .
The non-relativistic version of the Schrödinger equation , to add precision, is used in simple particles that move in electric fields (in this regard it is important to clarify that it does not apply in magnetic fields ).
The formulation and resolution of this equation is taught in training (university classes, courses, etc.) that emphasize phenomena and problems of chemistry and quantum physics . The objective is that students can understand it, master it and apply it to solve questions related to quantum dynamics .
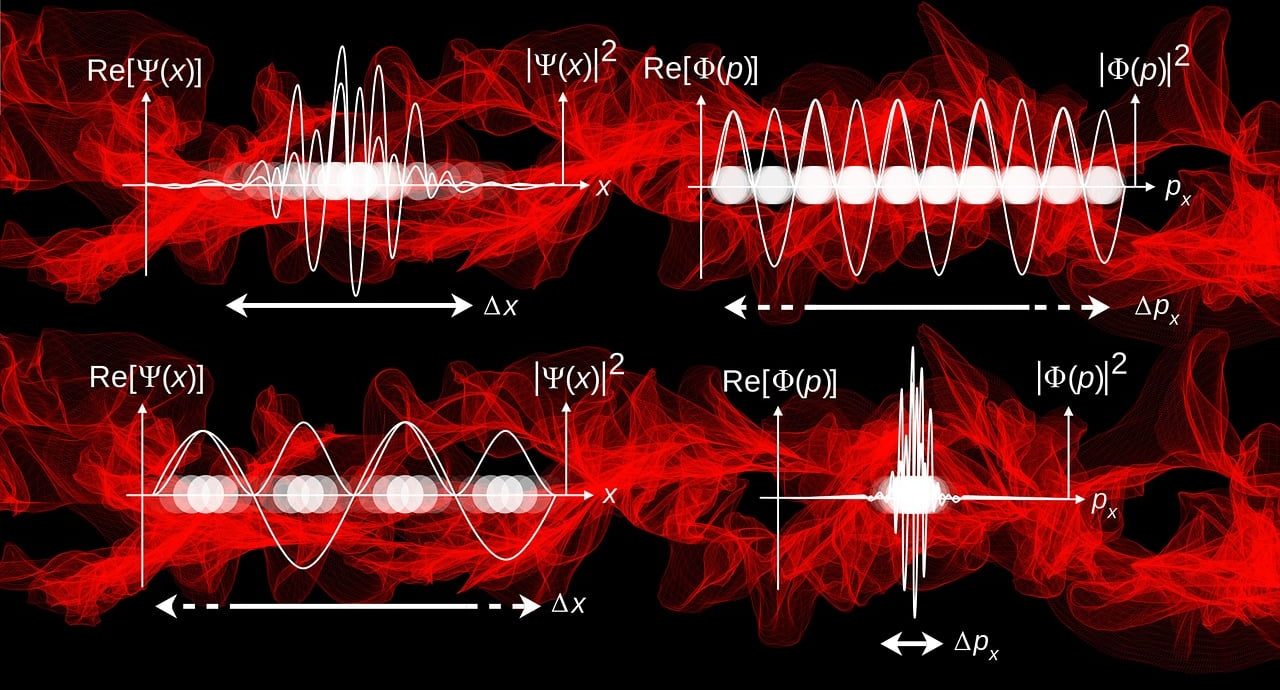
A particle traveling freely through free space is represented by a wave function capable of satisfying the non-relativistic root equation identified with the surname of physicist Erwin Schrödinger.
News linked to the Schrödinger equation
Research and approaches to the Schrödinger equation do not stop as the years go by. Thanks to developments, studies and tests that are carried out, new developments in this regard come to light with certain frequency.
Recently, to list some activities on the topic, a seminar has been given focused on the resolution possibilities offered by quantum computing for the Schrödinger equation . Taking advantage of artificial intelligence , on the other hand, several researchers based at a German university were able to solve the equation in an original way, achieving an unprecedented combination of computational efficiency and effectiveness . This announcement, as well as the achievement announced, contributes to quantum chemistry evolving more and more.
How waves propagate along an astrophysical disk is another answer that can be found through the Schrödinger equation . A professor named Konstantin Batygin has discovered that this resource can be used to detail how certain astronomical profile structures will evolve over the long term. According to the work of this scholar, the deformations that are evident on a large scale in a series of astrophysical disks exhibit behavior similar to that of particles .
