 The Latin word curvatūra came into our language as curvature . The concept refers to the condition of curved (bent or twisted). The idea of curvature is also used with respect to the deviation that a curved line has with respect to a straight line.
The Latin word curvatūra came into our language as curvature . The concept refers to the condition of curved (bent or twisted). The idea of curvature is also used with respect to the deviation that a curved line has with respect to a straight line.
For example: "The criminals tried to take advantage of the curvature of the wall to hide, but they were discovered" , "Poor body posture can cause, in the long term, the curvature of the spine " , "The curvature of the screen surprised the public" .
If someone talks about the curvature of a television, for example, they are referring to the fact that its screen is not straight. The curvature of a cell phone (mobile), for its part, is linked to its curved edges. In these cases, the curvature can represent both an aesthetic and functional aspect, or a fusion of both. Regardless of the purpose of this feature in an appliance, electronic device or automobile, among other products, fashion trends make it inevitable that its duration will be limited, so sooner or later the curvature is replaced by angular edges, and vice versa.
In the field of geometry and mathematics, curvature can be the magnitude or number that measures this quality. It is, in this framework, the amount that a geometric object deviates from a line or a plane.
The notion of curvature of space-time derives from the theory of general relativity , which postulates that gravity is an effect of the curved geometry of space-time. According to this theory, bodies that are in a gravitational field follow a curved path in space. The curvature of space-time is measured according to the so-called curvature tensor or Riemann tensor .
Curvature displacement , on the other hand, is a theory that indicates that a vehicle could travel at a speed greater than the speed of light based on a distortion that generates greater curvature in space-time .
There is a magnitude called the radius of curvature that is used to measure the curvature of an object belonging to geometry as if it were a surface, a curved line or, in more general terms, a differentiable variety found in a Euclidean space .
 If we take an object or a curved line as a reference, its radius of curvature is a geometric magnitude that we can define at each of its points, and is equivalent to the inverse of the absolute value of the curvature at all of them. We must not forget that curvature is the alteration that occurs in the direction of the tangent vector to a given curve as we move along it.
If we take an object or a curved line as a reference, its radius of curvature is a geometric magnitude that we can define at each of its points, and is equivalent to the inverse of the absolute value of the curvature at all of them. We must not forget that curvature is the alteration that occurs in the direction of the tangent vector to a given curve as we move along it.
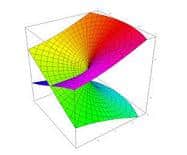
One of the measurements that we can make on a given surface is the Gaussian curvature , a number belonging to the set of real numbers that represents the intrinsic curvature for each of the regular points. It is possible to calculate it based on the determinants of the two fundamental shapes of the surface.
The first fundamental form of the surface is a 2-covariant tensor that presents symmetry and is defined in the tangent space to each of its points; This is the metric tensor (that is, rank 2, used for the definition of concepts such as volume, angle and distance) that induces the Euclidean metric on the surface. The second, however, is the projection of the covariant derivative that is carried out on the vector normal to the surface, and is induced by the first fundamental form.
Typically, the Gaussian curvature is different at each point on the surface and is related to its principal curvatures. The sphere is a special case of surface, since at all its points it has the same curvature.
