
A corollary is an inevitable conclusion or outcome. For example: the corollary of smoking several packs of cigarettes a day is a lung condition.
From the Latin corollarium , corollary is a proposition that is deduced from what has been previously demonstrated , so it does not require a particular proof . A corollary is understood to be an obvious or inevitable conclusion that follows from certain antecedents.
For example: “The corollary of smoking three packs of cigarettes a day is a lung disease” , “The team's relegation is the corollary of several years of poor management management” , “The senator's resignation after the scandal is nothing more than the corollary of the situation that broke out last Wednesday” , “The corollary could not be different: the three protesters were released due to lack of merit” .
In everyday language, a corollary appears as something logical or unavoidable if the preceding facts are taken into account . A soccer player argues with his team 's technical director during training. The next day, he publicly criticizes the coach. On the third day, he is absent from team practice without notice. The corollary of this situation is that the coach disaffects the player from the squad and stops taking him into account.
Corollary in logic
In the field of logic and mathematics, the corollary is the evidence of a theorem already proven, without the need to continue investing efforts in its demonstration.
If it is stated that all the interior angles of a square are right angles ( 90º ) and that all squares have four interior angles, a corollary of these statements is that the interior angles of a square add up to 360º .
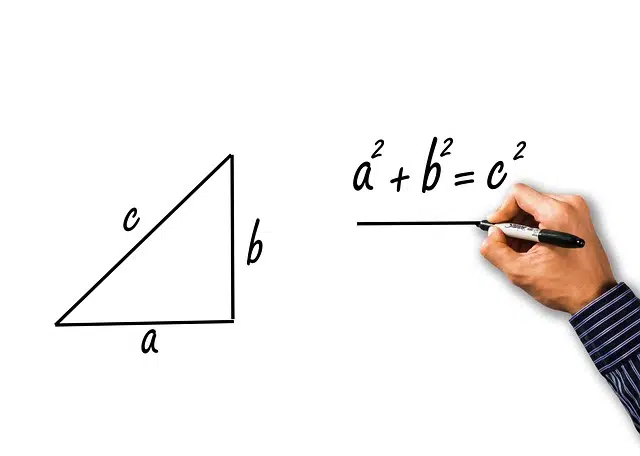
Corollaries emerge from the theorems.
The Pythagorean Theorem
From the well-known Pythagorean Theorem , which states that the sum of the squares of the legs of a right triangle returns the same value as squaring the hypotenuse, a corollary also emerges, which varies depending on whether we are talking about even numbers or odd. To develop this corollary, it is necessary to first establish the formula of the theorem.
The variable a is assigned the value of x ; b corresponds to x squared, minus 1, all divided by 2; a c , similar to b but adding 1 to the square instead of subtracting it. Having understood this development, it is possible to square each component and place them in the aforementioned equality.
Regarding even numbers, if we take for example a number and , the Pythagorean trio should be formed as seen in the image. In this case, a receives the value of y ; b is assigned the square of the result of y over 2, all but 1; The value of c is similar to b , but adding 1 to the previous square . With all this, we are once again in a position to define the equality that allows us to verify the Pythagorean Theorem.
Corollaries derived from the theorems of Thales of Miletus
The mathematician Thales of Miletus, a native of Greece and born in the 6th century BC, bequeathed two important theorems to geometry, each with their respective corollaries. The first of the theorems states that if a line is drawn parallel to any of the sides of a triangle, the resulting figure will be another triangle, similar to the first . Its corollary is the deduction that the proportion of the sides of the new triangle is also equivalent to that of the originals.
The second of Thales' theorems explains that if on a circle of diameter AC we choose any point, different from A and C , then the three will form a right triangle . From here two corollaries emerge:
1) since the distance between the center of the circle and any of the three points of the triangle is the same, then the median of the hypotenuse (segment between the center and point B ) will always measure half of the hypotenuse;
2) similar to the first, the radius of the circumference is equal to half of the hypotenuse, and the circumcenter is always located at its midpoint.
