Before proceeding to know the meaning of the term bisector, it is essential to discover its etymological origin. In this case, we can emphasize that it is a word that derives from Latin, since it is the result of the sum of the sum of several components of said language such as the following:
-The prefix «bi-«, which is synonymous with «two».
-The verb "secare", which can be translated as "cut".
-The suffix "-triz", which is used as a feminine agent.
Starting from this aforementioned formation we can determine what it means "that cuts into two equal parts."
The notion of bisector is used in the field of geometry to name that which divides or cuts something into two equal fragments . Generally the concept refers to the line that divides an angle into two identical segments.
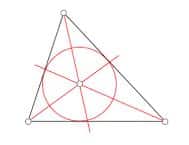A bisector of an angle , therefore, is a line that passes through its vertex and divides it into two parts. Regarding the points that are part of the plane, the points of the bisector constitute the geometric place that is equidistant from the two sides that form the angle.
When two lines intersect, they give rise to four consecutive angles . Their bisectors pass through the point of intersection and create four consecutive and right angles (that is, measuring 90º ).
The internal angles of a triangle , on the other hand, have three bisectors that intersect at the same point: the incenter , which is equidistant from the sides and constitutes the center of the circle that is formed inside the figure . This circle is tangent to the three sides of the triangle in question.
It should be noted that, from Thales' theorem , another theorem that involves a bisector follows: the internal angle bisector theorem of a triangle . This sentence indicates that, if we take a triangle, the ratio between two of its sides is equal to the ratio of the segments into which the third of the sides is divided by the passage of the bisector of the internal angle that is opposite.
What this means if we apply it to a formula is that of a triangle ABC, AD would be the bisector of the internal angle. Hence BA / AC becomes the same as BD / DC.
In addition to all of the above, we have to establish that there are those who confuse what the bisector is with the perpendicular bisector. However, it must be clear that they are not the same, they are different things:
-Thus, on the one hand, the perpendicular bisector is a line that is perpendicular to a segment. It also responds to the name symmetrical and is usually used to be able to establish what the circumcenter is.
-On the other hand, we must establish, as we have already explained, that the bisector is the ray that is responsible for dividing an angle into two equal parts.